表皮効果(交流抵抗・内部インダクタンス)の計算

1. 円柱導体(同軸ケーブルの中心導体)

2. 円筒(チューブ)導体

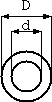
チューブ導体を同軸ケーブルの外部導体として使う場合は、外径と内径を逆に指定 します。

同軸ケーブルの外部導体として編組や横巻構造を使う場合は 同軸ケーブルの編組(横巻)外部導体の交流抵抗を参照 してください。

3. バイメタル導体(同軸ケーブルの銅覆鋼線)

必要な導体形状のフォームでパラメータを入力し「計算」をクリックします。

ケーブルの減衰は導体の交流抵抗から決まり、ケーブルの位相歪みは内部インダク タンスの周波数特性から決まりますが、これらの計算は導体の渦電流を求めること に帰着し、通常、次の３つの要因を考慮する必要があります。

1. 表皮効果
2. 近接効果
3. 隣接する他の導体の渦電流損失とその反作用

ここでは、表皮効果だけを考えれば済む、単独円柱、円筒導体について、 解析的に解けて、設計で頻繁に使われる重要なケースをまとめておきました。

単独で使われる導体というのはめったにありませんが、同軸ケーブルの内部導体は まさにこのケースになりますし、他の導体と遠く離れた導体は単独導体で近似できる ことに注意したください。

計算結果は、直流抵抗に対する交流抵抗の比、直流抵抗、交流抵抗、交流のインダ クタンスになります。ツインリード(ペア)を別にすれば、インダクタンスは導体の 内部インダクタンス であることに注意してください。

なお、空気の透磁率は 4e-7*π (H/m), 銅の導電率は 5.8e7 (S/m) です。 なお、空気の透磁率は 4e-7*π (H/m), 銅の導電率は 5.8e7 (S/m) です。