単層ソレノイドの自己インダクタンス

単層ソレノイドのコイルの平均半径、長さ、巻数、比透磁率を入力して「計算」釦を 押してください。

巻数を 0 にすると、長岡係数だけを計算します。

単層ソレノイドのインダクタンス計算は円筒状の無限に薄い電流シートを使った 非現実的なモデルに基づいていますが、実際には、 巻線の間隔(ピッチ)が極めて大きくない限り、 現実の巻線に十分近い値が得られます。

この円筒状電流シートモデルによる、 単層ソレノイドコイルの正確なインダクタンス計算を最初にやってのけたのは、 1879 年の Lorenz (注１) でした。 結果は、２つの楕円積分を含むもので、今ならどんなコンピュータでも簡単に計算 できますが、当時は級数展開による近似式を利用したり、数表化するしかなくて、 その数表化で最も成功したのが、 無限長ソレノイドの公式に対してコイル端の補正を行うという素直な発想の 「長岡公式(注２)」(Nagaoka's formula)でした。

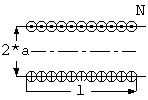
  L = K*μ*π*a*a*N*N/l
  ここに
	L = 単層ソレノイドコイルインダクタンス (H)
	K = 長岡係数 (Nagaoka coeeficient)
	  = 4/(3*π*sqrt(1-k^2))*((1-k^2)/k^2*K(k) - (1-2*k^2)/k^2*E(k) - k)
	k = 1 / sqrt(1 + (l/(2*a)^2)
	μ = 透磁率 (真空や非磁性体なら 4e-7*π)
	       π/2
	K(k) = ∫(1 / sqrt(1 - k^2 * sin(θ)^2)) * dθ
	       0
	       π/2
	E(k) = ∫sqrt(1 - k^2 * sin(θ)^2) * dθ
	       0
	a = コイルの半径 (m)
	l = コイルの長さ (m)
	N = コイルの巻き数

注

(1) Lorenz, Wied. Ann. 7, 161 (1879); B. of S.Sci. Paper 169, 117.
(2) Nagaoka, Jour. Coll. Sci. Tokyo 27, 18-33, art. 6 (1909); B. of S. Sci. Paper 169, 64.